Law of Sines & Cosines |
Prerequisites: Trig Equations.
The law of sines, and the law of cosines can be used to
solve oblique triangles (that is triangles without a right
angle). |
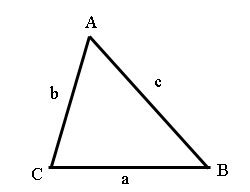 |
| It is important to know how to label triangles when
dealing with this topic. Each angle and side can be labeled
any letter (usually A, B, and C), as long as the side
opposite the angle is the same letter. Angles are upper-case,
and sides are lower-case. |
You can solve any oblique triangle in the following
cases:
- Two angles and a side (AAS or ASA)
- Two sides and an angle opposite one of them (SSA)
- Three sides (SSS)
- Two sides and their included angle (SAS)
The actual law of sines is as follows: |
 |
| With these, you plug in side lengths and angles to solve
a triangle. |
Ambiguous Case (SSA)
|
| Some triangles can not be solved for certain. It may
have, zero, one, or two solutions. Observe the following
example: |
 |
12 ÷ sin20.5° = 31 ÷ sinB
(12 ÷ sin20.5°)sinB = 31
sinB = 31 ÷ (12 ÷ sin20.5°)
sinB = 31 * (sin20.5° ÷ 12)
sinB =~ .9047
Now comes the ambiguous point. Since there are two points
on a unit circle between 0° and 180°, there are
therefore two possible solutions to the triangle.
So now you have two triangles. One where angle B is 115.22°
in one, and 64.78° on the other.
From there you solve the rest of each triangle. |
Think you are ready? Take the test! |



