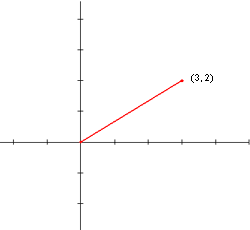Complex Numbers |
On a complex number plane, the standard
form of the equation is:
z = a +bi
The horizontal axis is called the real axis,
and the vertical is called the imaginary axis.
That is that one is what is normally the x axis, and the
other what is usually the y axis, respectively. To find
the point on the plane that the complex number represents,
you use the point (a, b). |
Definition of the Absolute Value of a Complex Number
|
The absolute value of the complex number
z = a + bi is:
|a + bi| = rt(a^2 + b^2) |
So if you have the complex number z = 3 + 2i, then you
would find the absolute value like this: |
rt(3^2 + 2^2)
rt(9 + 4)
rt(13) |
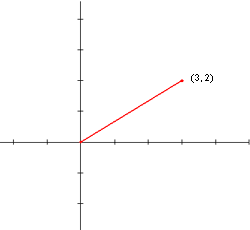
This is a graph of z = 3 + 2i |
Trigonometric Form of a Complex Number
|
In order to find
the trigonometric form of z = a + bi, you use the following
formula:
z = r(cosx + isinx)
where a = rcosx, b = rsinx, r = rt(a^2 + b^2), and tanx
= b ÷ a.
Vocab:
Here, r is the modulus of z, and x is the argument
of z. |
To find the trig form of the complex number z = 3 + 2i,
you would use r, which as we now know is equal to rt(13),
and then find out the value of x.
tanx = a ÷ b
tanx = 3 ÷ 2
x =~ 56.31°
In some problems, you might need to change the angle,
depending on what quadrant the complex number is located
in. In this case, we don't need to change the angle since
56.31° is in the same quadrant as the example. And
so...
z = rt(13)(cos56.31° + isin56.31°)
... is the trigonometric form of this complex number. |
Multiplication and Division of a Complex Number
|
Prerequisites:
Sum and Difference Formulas
Multiplication and division of complex numbers in trigonometric
form:
Where z
= r(cosx
+ isinx)
and z
= r(cosx
+ isinx)
are complex numbers...
Product:
z z
= rr[cos(x
+ x)
+ isin(x
+ x)]
Quotient:
z
÷ z
= (r
÷ r)[cos(x
+ x)
+ isin(x
+ x)]
z 
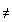0 |
Here is an example of a multiplication problem: |
z
= 3(cos(
÷ 3) + isin(
÷ 3))
z
= 4(cos(
÷ 6) + isin(
÷ 6))
Start by using the formula.
(3 * 4)(cos((
÷ 3) + (
÷ 6)) + isin((
÷ 4) + (
÷ 6))
Find the fractions' common denominators.
12(cos((2
÷ 6) + (
÷ 6)) + isin((3
÷ 12) + (2
÷ 12))
Combine like terms.
12(cos(3
÷ 6) + isin(5
÷ 12)
12(cos(
÷ 2) + isin(5
÷ 12)
Simplify the cosine and sine.
12(0 + i(.9659))
z
z
=~ 11.59i |
Powers of
Complex Numbers |
Besides using the
multiplication formula to solve powers, you can use DeMoivre's
Theorem.
If z = r(cosx + isinx)^n is a complex number and n is
a positive integer, then...
z^n = [r(cosx + isinx)]^n
z^n = r^n(cos(nx) + isin(nx)) |
Consider the following problem:
z = (1 - i)^12
Start by finding the r value:
r = rt(1² + (-1)²)
r = rt(2)
So now we must find the value of x.
tanx = 1 ÷ -1
tanx = -1
x = ÷
4
But since this complex number lies in qudarant 4, and
x is in quadrant 1, we will change it to -
÷ 4. Now we use DeMoivre's Theorem.
(1 - i)^12
rt(2)^12(cos(12(-
÷ 4)) + isin(12(-
÷ 4)))
rt(2)^12(-1 + i0)
64(-1 + 0i)
z = -64 |
